Benjamin RotenbergPHENIX Laboratory, French Nationwide Centre for Clinical Analysis (CNRS), and Sorbonne College, Paris, FranceNovember 18, 2024• Physics 17, 163The id of a brand new form of symmetry in statistical mechanics may assist scientists derive and interpret elementary relationships on this department of physics.
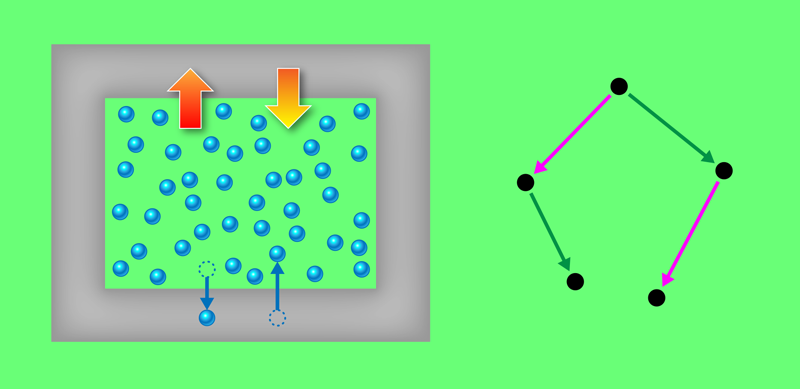
Determine 1: (Left) Within the so-called grand-canonical ensemble, a machine of debris (blue) is involved with a warmth and particle reservoir (grey). The machine keeps a relentless temperature and chemical possible via exchanging power and debris with the reservoir. Schmidt and associates have discovered that techniques similar to this one show off a up to now unidentified type of symmetry [1]. (Proper) This symmetry relates to adjustments in coordinates (black) that describe the positions and momenta of the machine’s debris. Those adjustments fulfill particular members of the family. Particularly, when two such transformations (red and inexperienced) are carried out successively, the order wherein they’re carried out impacts the general coordinates. Observable homes are left unchanged via those transformations, resulting in so-called hyperforce members of the family between the observables.
Determine 1: (Left) Within the so-called grand-canonical ensemble, a machine of debris (blue) is involved with a warmth and particle reservoir (grey). The machine keeps a relentless temperature and chemical possible via exchanging power and debris with the reservoir. Schmidt and associates have discovered that techniques similar to this one show off a up to now unidentified type of symmetry [1]. (Proper) This symmetry relates to adjustments in coordinates (black) that describe the positions and momenta of the machine’s debris. Those adjustments fulfill particular members of the family. Particularly, when two such transformations (red and inexperienced) are carried out successively, the order wherein they’re carried out impacts the general coordinates. Observable homes are left unchanged via those transformations, resulting in so-called hyperforce members of the family between the observables.×
Symmetry is a foundational thought in physics, describing homes that stay unchanged beneath transformations similar to rotation and translation. Spotting those invariances, whether or not intuitively or thru complicated arithmetic, has been pivotal in growing classical mechanics, the speculation of relativity, and quantum mechanics. For instance, the prestigious usual style of particle physics is constructed on such symmetry ideas. Now Matthias Schmidt and associates on the College of Bayreuth, Germany, have known a brand new form of invariance in statistical mechanics (the theoretical framework that connects the collective habits of debris to their microscopic interactions) [1]. With this discovery, the researchers be offering a unifying standpoint on delicate relationships between observable homes and supply a common manner for deriving new members of the family.
The concept that of conserved, or time-invariant, homes has roots in historical philosophy and was once an important to the upward thrust of contemporary science within the seventeenth century. Power conservation was a cornerstone of thermodynamics within the nineteenth century, when engineers exposed the hyperlink between warmth and paintings. Every other necessary form of invariance is Galilean invariance, which states that the rules of physics are similar in all reference frames transferring at a relentless pace relative to one another, leading to particular members of the family between positions and velocities in several frames. Its extension, Lorentz invariance, posits that the rate of sunshine is unbiased of the reference body. Einstein’s particular relativity is in keeping with Lorentz invariance, whilst his common relativity broadens the theory to all coordinate transformations. Those ultimate examples illustrate that invariance no longer handiest supplies members of the family between bodily observables however can form our working out of area, time, and different elementary ideas.
In 1918, the mathematician Emmy Noether proved {that a} conserved amount is related to each and every steady symmetry of a bodily machine [2, 3]. For instance, conservation of linear or angular momentum displays invariance beneath translations or rotations in area, while power conservation displays invariance beneath translations in time. This apparently summary theorem reshaped how the rules of physics are derived or even how “topic” and “interactions” are outlined. For example, the usual style of particle physics is a quantum box principle in keeping with the concept that of gauge invariance, the truth that the rules of physics are unchanged via positive transformations of the variables used to explain the rules. If that’s the case, the related symmetries aren’t as acquainted as spatial translations and rotations, however they guided the decision of the corresponding conserved amounts, as prescribed via Noether’s theorem.
Over the last few years, Schmidt and associates have put the facility of Noether’s theorem to paintings to acquire leads to the context of equilibrium statistical mechanics [4–6]. This department of physics offers with the homes of ensembles of microscopic configurations of a classical machine. One such ensemble is the grand-canonical ensemble, wherein the machine keeps a relentless temperature and chemical possible via exchanging power and debris with a warmth and particle reservoir (Fig. 1, left). Equilibrium statistical mechanics is the related conceptual framework for working out a big machine’s collective options, similar to its part diagram and different thermodynamic homes, in keeping with the microscopic interactions of its debris.
In that earlier paintings, Schmidt and associates presented an infinitesimal “phase-space transferring” operation, which transforms the positions and momenta of debris in a particular manner (Fig. 1, proper). The researchers used this operation and Noether’s theorem to derive precise members of the family for the correlations between forces provide within the machine and common observable homes. Such members of the family may also be expressed as averages of phase-space purposes. For instance, the correlation between the native density of exterior forces appearing at the machine and the native density of debris is the same as the gradient of the latter. The researchers coined such identities “hyperforce” members of the family.
Within the present find out about, Schmidt and associates have known the phase-space-shifting operation as a gauge transformation for microscopic states in equilibrium statistical mechanics. Importantly, this modification leaves the microstates and all corresponding phase-space purposes, together with all observable homes, unchanged. This sort of gauge invariance supplies a chic and environment friendly framework for rederiving and verifying hyperforce members of the family. Crucially, it additionally delivers a constant framework for working out those members of the family and a scientific solution to download new ones. The researchers illustrate their effects thru numerical simulations of a particular machine: one-dimensional laborious rods confined between two laborious partitions. In doing so, they display that gauge invariance could also be preserved when the use of a finite, as an alternative of infinitesimal, phase-space-shifting operation.
As famous via Schmidt and associates, the position of gauge transformations additionally resonates with different methods to compute statistical homes of particle-based techniques [7–10]. For instance, asking what would exchange beneath a slight adjustment of the coordinate machine isn’t so other from asking what would exchange beneath a slight motion of the debris. By means of extension, the exchange within the chance of positive microscopic states being provide, which is determined by their power, is expounded to the power exchange related to transferring debris. In flip, this chance exchange is correlated with the forces appearing at the debris as a result of pressure is the gradient of power with appreciate to particle place.
The researchers’ gauge-invariance framework may result in new force-based estimators of the native homes of those techniques, such because the native particle density or the radial distribution purposes quantifying the spatial correlations between debris. Such estimators may require fewer microscopic configurations to reach a goal accuracy, thereby lowering the computational price and corresponding carbon footprint. Long run instructions may come with inspecting dynamic homes out and in of equilibrium throughout the statistical mechanics of trajectories, as an alternative of microscopic configurations. Bearing in mind gauge invariance in that context would identify a more potent connection between equilibrium statistical mechanics and quantum mechanics. Past elementary paintings, the members of the family derived via the researchers, and ones but to be received from the proposed framework, may give upward push to new computational gear with packages in all fields wherein molecular simulations already play an very important position, from fabrics science to molecular biology.ReferencesJ. Müller et al., “Gauge invariance of equilibrium statistical mechanics,” Phys. Rev. Lett. 133, 217101 (2024).E. Noether, “Invariante variationsprobleme,” Nachr. Ges. Wiss. Gottingen, Math.-Phys. Kl 235 (1918); [English translation] “Invariant variation issues,” Transp. Principle Stat. Phys. 1, 186 (1971).N. Byers, “E. Noether’s discovery of the deep connection between symmetries and conservation rules,” arXiv:physics/9807044.S. Hermann and M. Schmidt, “Noether’s theorem in statistical mechanics,” Commun. Phys. 4, 176 (2021).S. Hermann and M. Schmidt, “Why Noether’s theorem applies to statistical mechanics,” J. Phys.: Condens. Matt. 34, 213001 (2022).S. Robitschko et al., “Hyperforce steadiness by means of thermal Noether invariance of any observable,” Commun. Phys. 7, 103 (2024).D. Borgis et al., “Computation of pair distribution purposes and 3-dimensional densities with a discounted variance concept,” Mol. Phys. 111, 3486 (2013).D. de las Heras and M. Schmidt, “Higher than counting: Density profiles from pressure sampling,” Phys. Rev. Lett. 120, 218001 (2018).B. Rotenberg, “Use the pressure! Diminished variance estimators for densities, radial distribution purposes, and native mobilities in molecular simulations,” J. Chem. Phys. 153, 150902 (2020).A. Purohit et al., “Drive-sampling strategies for density distributions as cases of mapped averaging,” Mol. Phys. 117, 2822 (2019).In regards to the WriterBenjamin Rotenberg is a French Nationwide Centre for Clinical Analysis (CNRS) senior researcher at Sorbonne College, France. He graduated in chemistry from École Normale Supérieure in 2004 and won his PhD from the Pierre and Marie Curie College in 2007. After a postdoc on the FOM Institute for Atomic and Molecular Physics, Netherlands, he began at CNRS in 2008. He was once a visiting professor on the College of Barcelona, Spain, the College of California, Berkeley, and the College of Freiburg, Germany, in addition to within the Helmholtz Zentrum Berlin. His analysis specializes in multiscale modeling of charged fluids and interfaces, in particular within the spaces of power and the surroundings, and he develops new strategies for numerical simulations.Topic AreasRelated Articles
Atomic and Molecular PhysicsQuantum Coherence Boosts Quantum WorkOctober 28, 2024By manipulating a nitrogen emptiness’s unmarried spin, researchers have proven that the extra coherent the machine is, the extra paintings may also be extracted from it. Learn Extra » Extra Articles














