Daedalus can have discovered a factor or two from a group of physicists in the United Kingdom and Switzerland.Taking ideas from fractal geometry and the strategic recreation of chess, they’ve created what they are saying is probably the most fiendishly tricky maze ever devised.
Led by means of physicist Felix Flicker of the College of Bristol in the United Kingdom, the gang has generated routes known as Hamiltonian cycles in patterns referred to as Ammann-Beenker tilings, generating advanced fractal mazes that, they are saying, describe an unique type of subject referred to as quasicrystals.
And it used to be all impressed by means of the motion of a Knight round a chess board.
“After we appeared on the shapes of the traces we built, we spotted they shaped extremely intricate mazes. The sizes of next mazes develop exponentially – and there are a vast choice of them,” Flicker explains.
“In a Knight’s excursion, the chess piece (which jumps two squares forwards and one to the correct) visits each and every sq. of the chessboard simply as soon as ahead of returning to its beginning sq.. That is an instance of a ‘Hamiltonian cycle’ – a loop thru a map visiting all preventing issues handiest as soon as.”An instance of an open Knight’s excursion of a chessboard, with visited squares shaded. For the excursion to be ‘closed’, the Knight wishes to finish on a sq. one Knight’s transfer from the place it began (so it could possibly go back to the beginning sq. and move across the board once more). (Ilmari Karonen/CC0/Wikimedia Commons)Quasicrystals are a type of subject handiest discovered very extraordinarily infrequently in nature. They are type of a odd hybrid of ordered and disordered crystals in solids.
In an ordered crystal – salt, or diamonds, or quartz – the atoms are organized in an excessively neat development that repeats in 3 dimensions. You’ll be able to take a bit of this lattice and superimpose it on some other, and they’re going to fit up completely.
A disordered, or amorphous, forged, is one through which the atoms are simply all higgledy-piggledy. Those come with glass and a few kinds of ice generally now not discovered on Earth.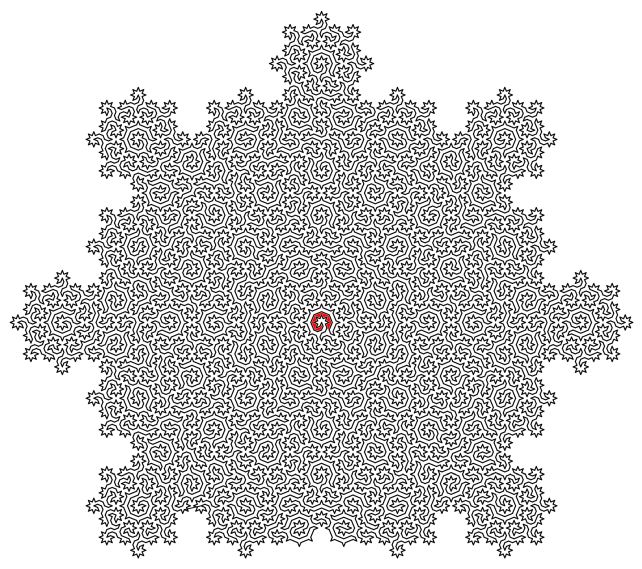
A maze generated by means of discovering a Hamiltonian cycle on an Ammann-Beenker tiling. Do not be disturbed. They are able to get a lot, a lot better and more difficult. An answer can also be noticed down beneath. (College of Bristol)A quasicrystal is a subject material through which the atoms shape a development, however the development does now not repeat completely. It would appear beautiful self-similar, however superimposed sections of the development is not going to fit up.
Those similar-looking however non-identical patterns are similar to a mathematical idea known as aperiodic tilings, which contain patterns of shapes that don’t identically repeat.
The well-known Penrose tiling is this kind of. The Ammann-Beenker tiling is some other.
The use of a collection of two-dimensional Ammann-Beenker tilings, Flicker and his colleagues, physicists Shobhna Singh of Cardiff College in the United Kingdom and Jerome Lloyd of the College of Geneva in Switzerland, generated Hamiltonian cycles that they are saying describe the atomic development of a quasicrystal.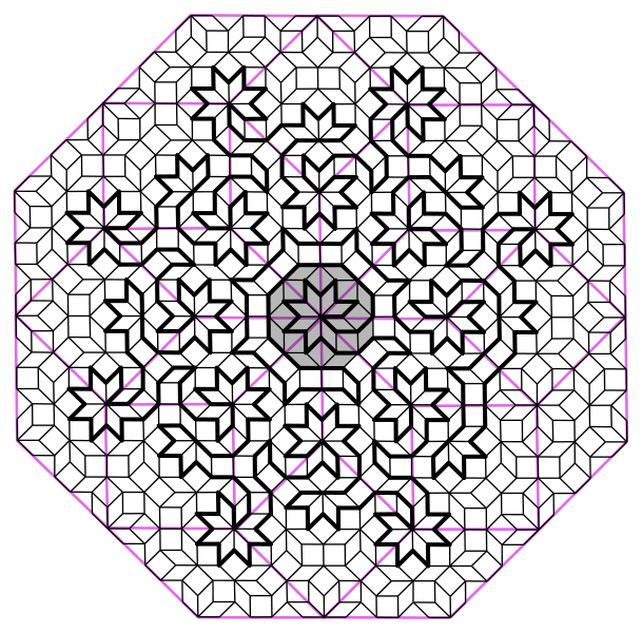
An Ammann-Beenker tiling with a thicker black line tracing out the Hamiltonian trail by means of visiting every vertex. The crimson traces aren’t a part of the tiling. (Singh et al., Phys. Rev. X, 2024)Their generated cycles consult with every atom within the quasicrystal handiest as soon as, connecting all of the atoms in one line that by no means crosses itself, however cleanly continues from starting to finish. And this can also be scaled infinitely, producing a kind of mathematical development referred to as a fractal, through which the smallest portions resemble the most important.
This line then naturally produces a maze, with a get started level and an go out. However the analysis has a ways larger implications past entertaining antsy kids in diners.
For one, discovering Hamiltonian cycles is terribly tricky. An answer that may permit for Hamiltonians to be known has the prospective to resolve many different difficult mathematical issues, from advanced course discovering techniques to protein folding.
And, curiously, there are implications for carbon seize by way of adsorption, an commercial procedure that comes to hoovering up molecules in a fluid by means of sticking them to crystals. If lets use quasicrystals for this procedure as an alternative, versatile molecules may just pack themselves extra tightly by means of mendacity alongside the Hamiltonian cycle therein.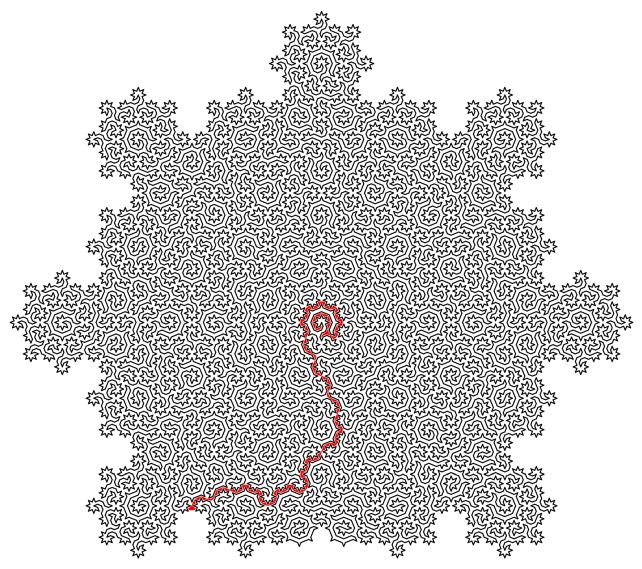
One imaginable technique to the maze above. (College of Bristol)”Our paintings additionally displays quasicrystals could also be higher than crystals for some adsorption packages,” Singh says.
“For instance, flexible molecules will to find extra tactics to land at the irregularly organized atoms of quasicrystals. Quasicrystals also are brittle, which means they readily destroy into tiny grains. This maximizes their floor space for adsorption.”
And when you occur to have a minotaur you want to stash away someplace, we predict we all know anyone who can assist.The analysis has been revealed in Bodily Assessment X.
